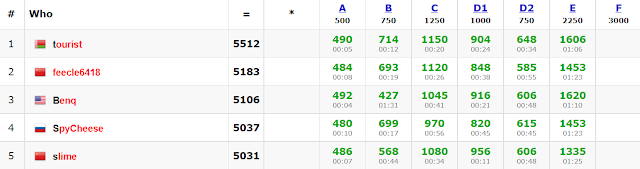
Codeforces Round 767 followed on Saturday (problems, results, top 5 on the left, analysis). I did not like the long statement of A and I did not immediately see the solution to B, so I've started solving the (relatively) easier problems in a weird order: D1, D2, C, A. When I solved these four, I saw that tourist already had all of them + problem B solved, so it became clear that I needed to go for the harder problems if I wanted to have a shot at the first place. We solved E roughly at the same time which did not change the situation, so I went all in on F, but unfortunately did not manage to finish in time.
- Given l and r, color all vertices with numbers between l and r black.
- Given l and r, color all vertices with numbers between l and r white.
- Given x, find the largest edge weight in the union of the shortest paths from x to all black vertices.
The first observation is somewhat natural: let's look at the incremental maximums of the original permutation. If their number k is even, then it's easy to find the required split: let's find the (k/2+1)-th incremental maximum, and let the first subsequence consist of all numbers before it, and the second subsequence of this number and all following number. Then each of the subsequences will have exactly k/2 incremental maximums, and those will be exactly the incremental maximums of the original permutation.
We can also notice the following "reverse" observation: each of the incremental maximums of the original permutation will be an incremental maximum of one of the two subsequences. But of course the subsequence may have additional incremental maximums. Let's call the incremental maximums of the original permutation the big ones, and all others the small ones.
Notice that we can always get rid of a small incremental maximum without affecting any other big or small incremental maximums: just move it to the other subsequence (where it will be hidden by the big incremental maximum that was hiding it in the original permutation), together with any additional small incremental maximums that appear when we remove this one.
Therefore if there is a solution to this problem where both subsequences have small incremental maximums, we can keep removing one from each until one of the subsequences has only big ones. So without loss of generality we can only look for solutions where the second subsequence has only big incremental maximums.
In a similar spirit to the above argument, we can also introduce new small incremental maximums by moving them from the other subsequence. Therefore the set of incremental maximums of the first subsequence can be any increasing subsequence of the original permutation.
Therefore the problem has been reduced to the following: does there exist an increasing subsequence of the given permutation such that it contains exactly k-m out of k big maximums, where m is its length?
Now we can assign a weight of 2 to all big maximums, and a weight of 1 to all other numbers, and our question simply becomes: "does there exist an increasing subsequence of weight k?"
Finally, we can notice that we can always decrease the weight of a subsequence by 2 by simply removing some elements, so it's enough to answer the question "what is the maximum weight of an increasing subsequence which has the same parity as k?" And this question can be answered by adapting a O(n*log(n)) algorithm for the longest increasing subsequence.
Notice how we first obtained a working understanding of the solution space here — that we can have any two disjoint incremental subsequences of the original permutation that cover all big maximums as the sequences of incremental maximums of the two parts — and then the actual algorithmic solution was not that hard to see.
Thanks for reading, and check back (hopefully) tomorrow for this week's summary!