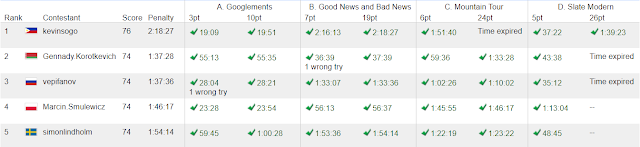
This week's contests were clustered on Sunday. In the morning, the first day of IOI 2017 took place in Tehran (problems, results, top 5 on the left, video commentary). The "classical format" problems wiring and train were pretty tough, so most contestants invested their time into the marathon-style problem nowruz. Three contestants have managed to gain a decent score there together with 200 on the other problems, so it's quite likely that they will battle for the crown between themselves on day 2. Congratulations Attila, Yuta and Mingkuan!
A few hours later, Codeforces Round 426 gave a chance to people older than 20 :) (problems, results, top 5 on the left). The round contained a bunch of quite tedious implementation problems, and Radewoosh and LHiC have demonstrated that they are not afraid of tedious implementation by solving 4 out of 5. Well done!
In my previous summary, I have raised a sportsmanship question, asking whether it's OK to bail out of an AtCoder contest without submitting anything. The poll results came back as 42% OK, 28% not OK, and 30% saying that the contest format should be improved. As another outcome of that post, tourist and moejy0viiiiiv have shared their late submission strategies that do not consider bailing out as a benefit, so I was kind of asking the wrong question :) I encourage you to read the linked posts to see how the AtCoder format actually makes the competition more enjoyable.
I have also mentioned a bunch of problems in that post, so let me come back to one of them: you are given two rooted trees on the same set of 105 vertices. You need to assign integer weights to all vertices in such a way that for each subtree of each of the trees the sum of weights is either 1 or -1, or report that it's impossible.
First of all, we can notice that the value assigned to each vertex can be computed as (the sum of its subtree) - (the sum of subtrees of all its children). Since all said sums are either -1 or 1, the parity of this value depends solely on the parity of the number of children. So we can compare said parities in two trees, and if there's a mismatch, then there's definitely no solution.
Now, after playing a bit with a few examples, we can start to believe that in case all parities match, there is always a solution. During the actual contest I've implemented a brute force to make sure this is true. Moreover, we can make an even stronger hypothesis: there is always a solution where all values are -1,0 or 1. Again, my brute force has confirmed that this is most likely true.
For vertices where the value must be even, we can assume it's 0. For vertices where the value must be odd, we have two choices: -1 or 1. Let's call the latter odd vertices.
Our parity check guarantees that each subtree of each tree will have an odd number of odd vertices, in order to be able to get -1 or 1 in total. So we must either have k -1's and k+1 1's, or k+1 -1's and k 1's. Here comes the main idea: in order to achieve this, it suffices to split all odd vertices into pairs in such a way that in each subtree all odd vertices but one form k whole pairs, and each pair is guaranteed to have one 1 and one -1.
Having said that idea aloud, we can very quickly find a way to form the pairs: we would just go from leaves to the root of the tree, and each subtree will pass at most one unpaired odd vertex to its parent. There we would pair up as many odd vertices as possible, and send at most one further up.
Since we have not one, but two trees, we will get two sets of pairs. Can we still find an assignment of 1's and -1's that satisfies both sets? It turns out we can: the necessary and sufficient condition for such assignment to exist is for the graph formed by the pairs to be bipartite. And sure enough, since the graph has two types of edges, and each vertex has at most one edge of each type, any cycle must necessarily have the edge types alternate, and thus have even length. And when all cycles have even length, the graph is bipartite.
Looking back at the whole solution, we can see that the main challenge is to restrict one's solution in the right way. When we work with arbitrary numbers, there are just too many dimensions in the problem. When we restrict the numbers to just -1, 0, and 1, the problem becomes more tractable, and it becomes easier to see which ideas work and which don't. And when we add the extra restriction in form of achieving the necessary conditions by pairing up the vertices, the solution flows very naturally.
Thanks for reading, and check back next week!
A few hours later, Codeforces Round 426 gave a chance to people older than 20 :) (problems, results, top 5 on the left). The round contained a bunch of quite tedious implementation problems, and Radewoosh and LHiC have demonstrated that they are not afraid of tedious implementation by solving 4 out of 5. Well done!
In my previous summary, I have raised a sportsmanship question, asking whether it's OK to bail out of an AtCoder contest without submitting anything. The poll results came back as 42% OK, 28% not OK, and 30% saying that the contest format should be improved. As another outcome of that post, tourist and moejy0viiiiiv have shared their late submission strategies that do not consider bailing out as a benefit, so I was kind of asking the wrong question :) I encourage you to read the linked posts to see how the AtCoder format actually makes the competition more enjoyable.
I have also mentioned a bunch of problems in that post, so let me come back to one of them: you are given two rooted trees on the same set of 105 vertices. You need to assign integer weights to all vertices in such a way that for each subtree of each of the trees the sum of weights is either 1 or -1, or report that it's impossible.
First of all, we can notice that the value assigned to each vertex can be computed as (the sum of its subtree) - (the sum of subtrees of all its children). Since all said sums are either -1 or 1, the parity of this value depends solely on the parity of the number of children. So we can compare said parities in two trees, and if there's a mismatch, then there's definitely no solution.
Now, after playing a bit with a few examples, we can start to believe that in case all parities match, there is always a solution. During the actual contest I've implemented a brute force to make sure this is true. Moreover, we can make an even stronger hypothesis: there is always a solution where all values are -1,0 or 1. Again, my brute force has confirmed that this is most likely true.
For vertices where the value must be even, we can assume it's 0. For vertices where the value must be odd, we have two choices: -1 or 1. Let's call the latter odd vertices.
Our parity check guarantees that each subtree of each tree will have an odd number of odd vertices, in order to be able to get -1 or 1 in total. So we must either have k -1's and k+1 1's, or k+1 -1's and k 1's. Here comes the main idea: in order to achieve this, it suffices to split all odd vertices into pairs in such a way that in each subtree all odd vertices but one form k whole pairs, and each pair is guaranteed to have one 1 and one -1.
Having said that idea aloud, we can very quickly find a way to form the pairs: we would just go from leaves to the root of the tree, and each subtree will pass at most one unpaired odd vertex to its parent. There we would pair up as many odd vertices as possible, and send at most one further up.
Since we have not one, but two trees, we will get two sets of pairs. Can we still find an assignment of 1's and -1's that satisfies both sets? It turns out we can: the necessary and sufficient condition for such assignment to exist is for the graph formed by the pairs to be bipartite. And sure enough, since the graph has two types of edges, and each vertex has at most one edge of each type, any cycle must necessarily have the edge types alternate, and thus have even length. And when all cycles have even length, the graph is bipartite.
Looking back at the whole solution, we can see that the main challenge is to restrict one's solution in the right way. When we work with arbitrary numbers, there are just too many dimensions in the problem. When we restrict the numbers to just -1, 0, and 1, the problem becomes more tractable, and it becomes easier to see which ideas work and which don't. And when we add the extra restriction in form of achieving the necessary conditions by pairing up the vertices, the solution flows very naturally.
Thanks for reading, and check back next week!